Video: Ինչու են եռանկյունաչափական նույնականությունները օգտակար հավասարումներ լուծելու համար:
2024 Հեղինակ: Lynn Donovan | [email protected]. Վերջին փոփոխված: 2023-12-15 23:48
Ինքնություններ մեզ հնարավորություն է տալիս պարզեցնել բարդ արտահայտությունները: Դրանք հիմնական գործիքներն են եռանկյունաչափություն, որն օգտագործվում է եռանկյունաչափական հավասարումների լուծման մեջ , ճիշտ այնպես, ինչպես ֆակտորինգը, ընդհանուր հայտարարի գտնելը և հատուկ բանաձևերի օգտագործումը հիմնական գործիքներն են լուծում հանրահաշվական հավասարումներ.
Այնուհետև ի՞նչն է դարձնում եռանկյունաչափական հավասարումը նույնականություն:
Մաթեմատիկայի մեջ, եռանկյունաչափական ինքնություններ հավասարություններ են, որոնք ներառում են եռանկյունաչափական ֆունկցիաները և ճշմարիտ են տեղի ունեցող փոփոխականների յուրաքանչյուր արժեքի համար, որտեղ սահմանված են հավասարության երկու կողմերը: Երկրաչափական առումով սրանք են ինքնությունները ներառում է մեկ կամ մի քանի անկյունների որոշակի գործառույթներ:
Նաև գիտեք, որո՞նք են եռանկյունաչափական հավասարումները: Ա եռանկյունաչափական հավասարում ցանկացած է հավասարումը որը պարունակում է ա եռանկյունաչափական ֆունկցիան։ Ինչպես նշված է Եռանկյունաչափական Ինքնություններ, ա եռանկյունաչափական հավասարում որը ճիշտ է ցանկացած անկյան համար, կոչվում է a եռանկյունաչափական ինքնությունը։ Կան ուրիշներ հավասարումներ , սակայն, դա ճիշտ է միայն որոշակի անկյունների համար:
Նմանապես կարելի է հարցնել՝ ո՞րն է եռանկյունաչափական ինքնությունները լուծելու ամենահեշտ ձևը:
ՔԱՅԼ 1. Փոխարկեք բոլոր վայրկյանները, csc-ը, cot-ը և tan-ը sin և cos-ի: Դրա մեծ մասը կարելի է անել՝ օգտագործելով գործակից և փոխադարձ ինքնությունները . ՔԱՅԼ 2. Ստուգեք բոլոր անկյունները գումարների և տարբերությունների համար և օգտագործեք համապատասխանը ինքնությունները դրանք հեռացնելու համար: ՔԱՅԼ 3. Ստուգեք անկյունների բազմապատիկները և հեռացրեք դրանք՝ օգտագործելով համապատասխան բանաձևերը:
Ինչի՞ն է հավասար մեղքը 2x:
sin2x =( մեղք x)2=12(1−cos( 2x )).
Խորհուրդ ենք տալիս:
Ինչու են դեպքերի դիագրամները օգտակար:
Միասնական մոդելավորման լեզու (UML) օգտագործելիս օգտագործման դեպքերի դիագրամն օգնում է ձեզ հասկանալ, թե ինչպես կարող է օգտվողը փոխազդել ձեր մշակած համակարգի հետ: Եվ ի վերջո, դա պետք է օգնի ձեր թիմին սահմանել և կազմակերպել պահանջները: Փոխարենը, դրանք ներկայացնում են բարձր մակարդակի ակնարկ, թե ինչպես են առնչվում օգտագործման դեպքերը, դերակատարները և ձեր համակարգը
Ինչու՞ է օգտակար ծրագրակազմը կարևոր:
Օպերացիոն համակարգերը վերահսկում են համակարգչային տեխնիկան և գործում են որպես ինտերֆեյս կիրառական ծրագրերի հետ: Utilitysoftware-ն օգնում է կառավարել, պահպանել և վերահսկել համակարգչային ռեսուրսները: Օգտակար ծրագրերի օրինակներ են հակավիրուսային ծրագրակազմը, պահեստային ծրագրակազմը և սկավառակի գործիքները
Ինչու՞ է Schottky դիոդը օգտակար բարձր հաճախականության ուղղման համար:
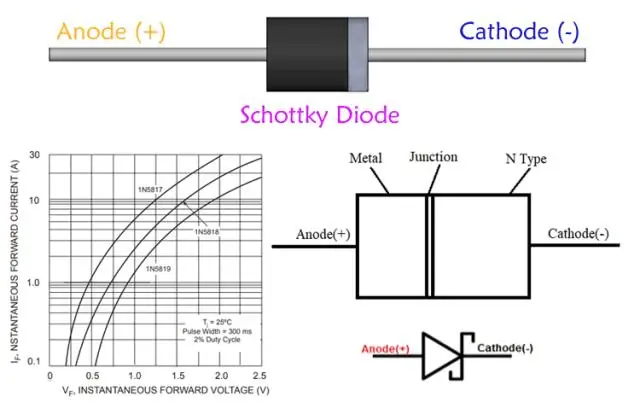
Schottky diode հավելվածներ. Էլեկտրաէներգիայի ուղղիչ. Schottky դիոդները նույնպես օգտագործվում են աշիղ ուժային ուղղիչներ: Դրանց հոսանքի բարձր խտությունը և առաջընթաց լարման ցածր անկումը նշանակում են, որ ավելի քիչ էներգիա է վատնում, քան օգտագործվում էին մի շարք PN միացման դիոդներ: Շոտկիդիոդները հակված են ունենալ բարձր հակադարձ արտահոսքի հոսանք
Ինչու է տասնվեցականը օգտակար համարակալման համակարգ:
Տասնվեցական համակարգը սովորաբար օգտագործվում է ծրագրավորողների կողմից՝ հիշողության մեջ տեղանքները նկարագրելու համար, քանի որ այն կարող է ներկայացնել յուրաքանչյուր բայթ (այսինքն՝ ութ բիթ) որպես երկու հաջորդական տասնվեցական թվանշան՝ ութ թվերի փոխարեն, որոնք կպահանջվեն երկուական (այսինքն՝ բազային 2) թվերը և երեք թվանշան, որոնք կպահանջվեն տասնորդականով
Ինչու են գեներատորները օգտակար:
Գեներատորները Python-ի կարևոր մասն էին այն պահից, երբ դրանք ներկայացվեցին PEP 255-ով: Գեներատորի գործառույթները թույլ են տալիս հայտարարել գործառույթ, որն իրեն պահում է կրկնվողի նման: Նրանք ծրագրավորողներին թույլ են տալիս արագ, հեշտ և մաքուր ձևով կրկնել: Իտերատորը օբյեկտ է, որի վրա կարելի է կրկնել (շրջել):